Конспект урока по теме: "Умножение дробей"

Урок обобщения и систематизации по теме «Умножение дробей»

Характеристика урока.

Тема: Умножение дробей

Тип урока: урок обобщения и систематизации.

Учебник: Математика: учеб. для 6 кл. общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. — 12-е изд., стереотип. – М.: Мнемозина, 2007.- 356 с: ил. (Глава 1, §3, п.13 – п.16)

Учебная задача: Обобщить и систематизировать знания и умения учащихся по теме «Умножение дробей».

Диагностируемые цели: в результате урока ученик:

Знает: Правило умножения дроби на натуральное число; правило умножения дроби на дробь; правило умножения смешанных чисел; правило нахождения дроби от числа; свойства умножения дробей; правило умножения смешенного числа на натуральное число.

Понимает взаимосвязь между понятиями, правилами в данной теме.

Умеет решать примеры на умножение дроби на натуральное число, умножение дроби на дробь, умножение смешанных чисел, нахождение дроби от числа, умножение смешенного числа на натуральное число. Решать различные задачи на применение изученной теории.

Методы обучения: репродуктивный, частично-поисковый, эвристическая беседа.

Средства: мел, доска, учебник, канва-таблица, плакат с канвой-таблицей.

Форма работы: фронтальная и индивидуальная.

Структура работы:

Мотивационно-ориентировочная часть (1 мин)

Содержательная часть (29 мин)

Рефлексивно-оценочная часть (10 мин)

Ход урока

I. Мотивационно-ориентировочная часть.

Учитель: Здравствуйте, ребята, садитесь. Мы заканчиваем изучение темы умножение дробей. Сегодня урок посвятим повторению. Поможет нам таблица, которую вы получили. Работать вы будете на этом листке, тетради на уроке нам не понадобятся. Образец таблицы у меня на доске. Давайте внимательно рассмотрим таблицу. Каждое окно таблицы имеет свой номер, задания отмеченные звёздочкой решает тот, кто идёт вперёд, с классом эти задания решать не будем, так же эти задания вы можете выполнить дома при подготовке к контрольной работе.

На следующем уроке вы пишите контрольную работу.

Постановка учебной задачи урока.

Поэтому целью нашего урока будет подготовка к контрольной работе.

II. Содержательная часть.

Учитель: Итак, внимание, ребята, начинаем с правила умножения дробей. Как умножить дробь на дробь?

Дети: Чтобы умножить дробь на дробь, надо:

Найти произведение числителей и произведение знаменателей этих дробей;
Первое произведение записать числителем, а второе – знаменателем.

Учитель: Запишем это правило с помощью букв. Если нам дана дробь 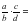(дробь a деленная на b, умноженная на дробь c деленная на d) чему будет равен результат?

Дети: Дроби, в числители которой произведение а и с, а в знаменателе произведение b и d 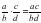(записывается в таблицу)

Учитель: Рассмотрим первый пример .

(Ученик выходит к доске)

Учитель: Что мы делаем первым шагом?

Ученик: Перемножаем числители и записываем в числитель, перемножаем знаменатели и записываем в знаменатель.

Учитель: Верно. Выполняй.

Ученик: .

Учитель: Что мы выполняем следующим шагом?

Ученик: Сокращаем.

Учитель: Верно.

Ученик:

Учитель: Молодец, спасибо. Второй пример выполните самостоятельно и скажите мне только ответ. Поднимите руку, кто уже решил?

(ребята, выполнившие задание поднимают руку)

Дети: ответ 0,3

Учитель: У кого получился другой ответ? Верно, 0,3 — это правильный ответ. Теперь будем работать во втором «окне». Повторим правило умножения дроби на натуральное число. Как умножить дробь на натуральное число?

Дети: Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменения.

Учитель: Молодец. Запишем это правило с помощью букв во второе окно таблицы. Если нам дана дробь а деленное на b и умноженная на натуральное число с, то как мы можем записать результат умножения в?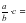

Дети: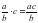

Учитель: Молодцы. Выполните первый пример самостоятельно.

Дети:

Учитель: Верно. А теперь решим у доски.

Как будешь решать этот пример?

Ученик: Числитель умножу на натуральное число, а знаменатель оставлю без изменения, выполню сокращение. Выделю целую часть.

Учитель: Молодец. А помните ли вы правило умножения смешенных чисел? Как умножить смешенное число на смешенное число?

Дети: Для того чтобы выполнить умножение смешанных чисел, надо записать их в виде неправильной дроби, а затем воспользоваться правилом умножения дробей.

Учитель: Хорошо. Тогда переходим работать в третье «окно». Решаем первый пример у доски.

Ученик:

Учитель: Хорошо. Пример под буквой б выполните самостоятельно.

Дети: ответ

Учитель: Под буквой в выполним у доски. Что нужно сделать со смешанными числами?

Ученик: Перевести в неправильную дробь.

Учитель: Верно. А как выполнить умножение трех дробей

Ученик: Нужно все три дроби записать под одной чертой, т.е. найду произведение числителей и поизведение знаменателей этих дробей; первое произведение записать числителем, а второе – знаменателем, выполнить сокращение, если это возможно, а затем записать ответ.

Учитель: Выполняй.

Ученик:

Учитель: Молодец. Правило умножения дробей мы повторили, а где оно применяется?

Дети: При решении задач.

Учитель: Верно. Скажите как найти дробь от числа?

Дети: Чтобы найти дробь от числа, нужно умножить число на эту дробь.

Учитель: Теперь давайте запишем это правило в таблицу.

(число)∙(дробь)

А сейчас выполним следующее задание: Найти от 25 кг

Ученик:

Учитель: Верно. Ребята, не забываем подписать величину. Теперь решим задачу.

О каких величинах говориться в задаче

Ученик: О длине ломаной, длине отрезков из которых она состоит

Учитель: Что известно?

Ученик: Длина ломаной 11 дм, длина первого отрезка равна 70% длины всей ломаной

Учитель: Что требуется найти?

Ученик: Длину второго отрезка

Учитель: Как ты думаешь что нужно сделать первым действием?

Ученик: Сначала перевести 70% в десятичную дробь, а затем

(дм) – длина первого отрезка

11-7,7=3,3(дм) – длина второго отрезка

Ответ: 3,3 дм

Учитель: Верно. Подумай, как можно решить эту задачу другим способом.

Ученик: 100%-70%=30% — составляет второй отрезок

110,3=3,3(дм) – длина второго отрезка

Учитель: Правильно. Садись. Кроме нахождения дроби от числа вы научились применять распределительное свойство умножения для решения уравнений, упрощения выражений и боле простых вычислений. Вспомним это свойство и запишем его в таблицу.

Дети: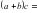

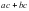
Учитель: А в другую сторону?

Дети: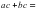

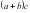
Учитель: Задание упростить выражение, решим первый пример устно.

Дети:

Учитель: Следующий пример решите самостоятельно.

Дети: Ответ

Учитель: Под буквой в решим у доски. Как ты будешь упрощать это выражение?

Ученик: Воспользуюсь распределительным свойством умножения и вынесу общий множитель за скобки. Выполню действия в скобках.

Учитель: Молодец. Еще мы применяем распределительное свойство умножения при решении уравнений. Переходим к шестому «окну»

Как будешь решать уравнение?

Ученик: Сначала раскрою скобки, применив распределительное свойство умножения.

Ответ:

Учитель: Хорошо. Решим следующее уравнение. Чем воспользуешься?

Ученик: Распределительным свойством, но в другую сторону.

Ответ: 7

Учитель: Хорошо. Ребята, посмотрите как помогает умножение дробей решать разные задания. Давайте проверим как вы научились решать задачи. Решим задачу №1. Прочитай, пожалуйста.

Ученик: Длина бревна 6,4 м. Сначала отпилили бревна, а затем 0,6 остатка. Найдите длину оставшейся после этого части бревна.

Учитель: О каких величинах говориться в задаче

Ученик: О длине бревна, длине частей.

Учитель: Что известно?

Ученик: Длина бревна 6, 4 м, длина первого отпила длины всего бревна, второго отпила – 0,6 остатка.

Учитель: Что требуется найти?

Ученик: Длину третьего.

Учитель: Как будешь решать задачу?

Ученик:

6,4-2,4=4(м) – осталось после первого отпила;

40,6=2,4(м) – отпилили во второй раз;

4-2,4=1,6(м) – осталось.

Ответ: 1,6 м

Учитель: А теперь решим вторую задачу.

Ученик: С огорода собрали 50кг томатов и кг моркови. В столовую отправили собранных томатов и моркови. Сколько килограммов овощей отправили в столовую?

Учитель: Как будешь решать?

Ученик: 50 — килограммов томатов отправили в столовую

–

50 + – килограммов овощей отправили в столовую.

50 + = (50+ 81=(кг) отправили в столовую.

Ответ: 72 кг

III. Рефлексивно-оценочная часть.

Учитель: Ребята, какова цель нашего урока.

Дети: Подготовка к контрольной работе, повторение темы «Умножение дробей»

Учитель: Достигли ли мы этой цели?

Дети: Да.

Учитель: А какие правила мы повторили?

Дети: Правило умножения дроби на натуральное число; правило умножения дроби на дробь; правило умножения смешанных чисел; правило нахождения дроби от числа; свойства умножения дробей; правило умножения смешенного числа на натуральное число.

Учитель: Хорошо. Ребята, внимание, домашнее задание записано с обратной стороны листа. Всё то, что мы сегодня решали и домашнее задание поможет подготовиться к контрольной работе, которая состоится в пятницу. Домашнее задание выполняем в тетрадях!

А сейчас проверочная работа – тест. На четвертинке листочка напишите фамилию и вариант: 1, 2.

Спасибо, урок окончен.

1вариант

1.Чему равно произведение 5 и ?

1). 2). 3). 4).

2. Найдите площадь квадрата со стороной

1). ² 2). ² 3). ² 4). ²

3. Вычислите:

1). 2). 3). 4). 5

4.Найдите произведение

1). 2). 3). 4).

5. Вычислите:

1). 2). 3). 4). 3

6.Вычислить удобным способом:

1). 2). 3). 4).

2 вариант

1.Чему равно произведение 3 и ?

1). 2). 3). 4).

2. Найдите площадь квадрата со стороной

1). ² 2). ² 3). ² 4). ²

3. Вычислите:

1). 2). 3). 4). 11

4.Найдите произведение

1). 2). 3). 4).

5. Вычислите:

1). 2). 3). 4). 1

6.Вычислить удобным способом:

1). 55 2). 3). 4).

Умножение дробей

1.Умножение дробей

2.Умножение дробей на натуральное число

3. Умножение смешанных чисел

А)

Б) =

___________________________

В)^*

___________________________

А) 1

_____________________________________

Б)

_____________________________________

В)

____________________________________

Г)^*

____________________________________

А) =

_______________________

Б)=

_______________________

Применение умножения дробей

4. Решение задач на нахождение дроби от числа	5. Упрощение выражений	6. Решение уравнений

А) Найти от 25 кг ______________________________ Б)^* Найти 0,8% от 84,5 га ____________________________________ В)^* Найти л ____________________________________ Г) Ломаная состоит из двух отрезков и имеет длину 11 дм. Первый отрезок равен 70% всей ломаной. Найдите длину второго отрезка. ______________________________ ______________________________ ______________________________ Ответ:	А) ______ Б) ____________________В) _______________________________________________________________________________________________________________________	А) ________________________ ________________________ ________________________ ________________________ Ответ:____________________ Б) 7 ________________________ ________________________ ________________________ ________________________ Ответ:____________________

Задача 1: Длина бревна 6,4 м. Сначала отпилили бревна, а затем 0,6 остатка. Найдите длину оставшейся после этого части бревна.

________________________________________________________________________

Ответ: __________________________________________________________________

Задача 2: С огорода собрали 50кг томатов и кг моркови. В столовую отправили собранных томатов и моркови. Сколько килограммов овощей отправили в столовую?

________________________________________________________________________

Ответ: __________________________________________________________________

Домашнее задание

п. 13-15
Найдите произведение:

Найдите значение выражения
На складе было 270 т картофеля. Вначале вывезли этого картофеля, а во второй раз вывезли 0,45 того, что вывезли в первый раз. Какую часть всего картофеля вывезли во второй раз? Сколько тонн картофеля осталось на складе?