
16.10.2015г. Классная работа. Геометрический смысл производной. (решение задач)

Задача №1.
На рисунке изображён
график функции y=f(x) и
касательная к нему в точке
с абсциссой x 0 . Найдите
значение производной
функции f(x) в точке x 0 .

Задача №2.
На рисунке изображён график
функции y=f(x) и касательная
к нему в точке с абсциссой x 0 .
Найдите значение производной
функции f(x) в точке x 0 .
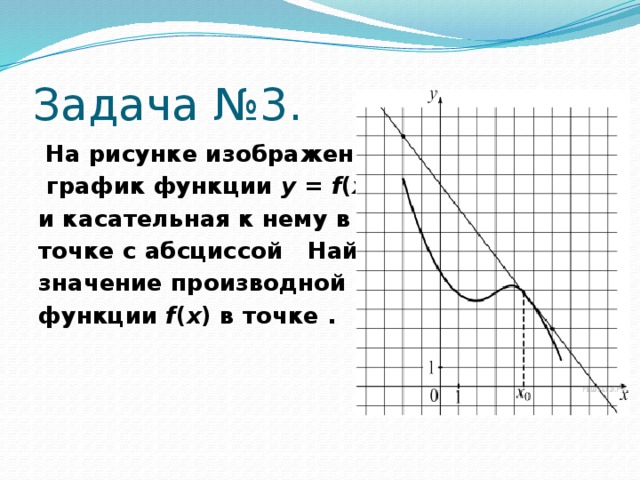
Задача №3.
На рисунке изображены
график функции y = f ( x )
и касательная к нему в
точке с абсциссой Найдите
значение производной
функции f ( x ) в точке .
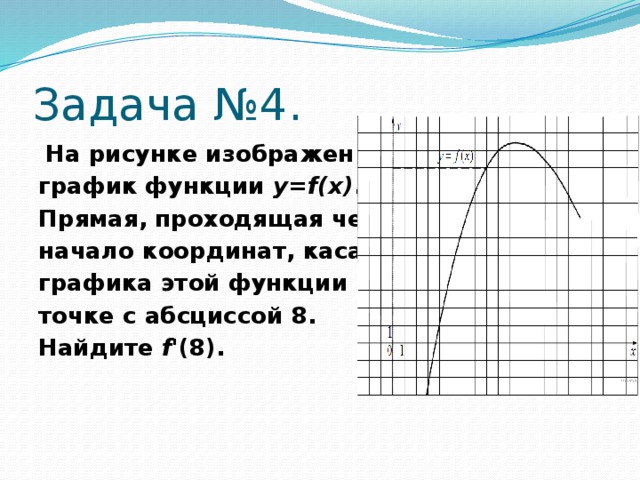
Задача №4.
На рисунке изображен
график функции y=f(x) .
Прямая, проходящая через
начало координат, касается
графика этой функции в
точке с абсциссой 8.
Найдите f’ (8).
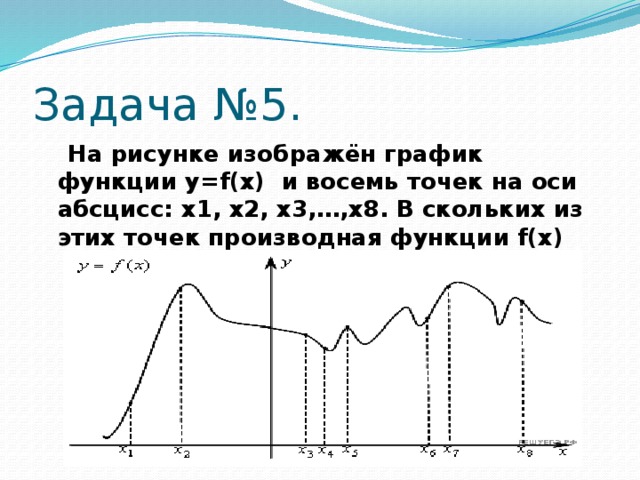
Задача №5.
На рисунке изображён график функции у=f(x) и восемь точек на оси абсцисс: х1, х2, х3,…,х8. В скольких из этих точек производная функции f(x) положительна?
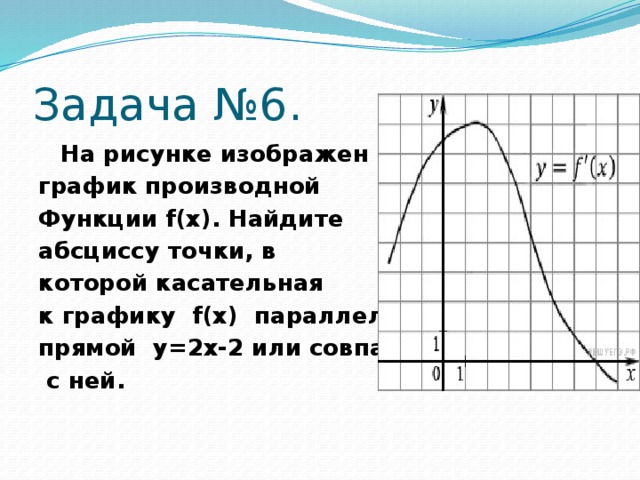
Задача №6.
На рисунке изображен
график производной
Функции f(x). Найдите
абсциссу точки, в
которой касательная
к графику f(x) параллельна
прямой y=2x-2 или совпадает
с ней.
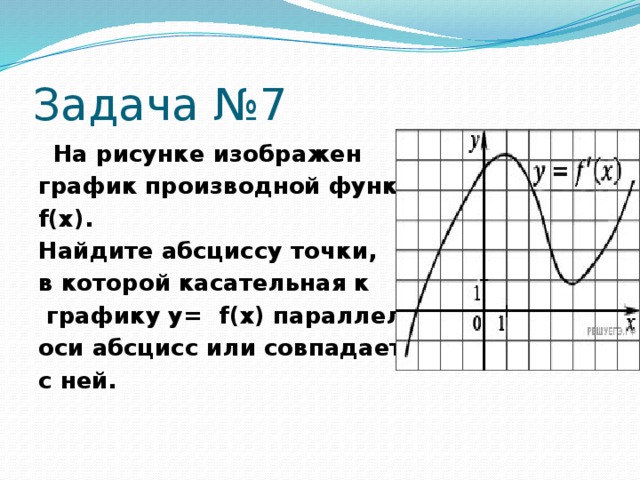
Задача №7
На рисунке изображен
график производной функции
f(x).
Найдите абсциссу точки,
в которой касательная к
графику y= f(x) параллельна
оси абсцисс или совпадает
с ней.

Задача №8.
Прямая y=-4x-11 является касательной к графику функции y=x^3+7x^2+7x-6. Найдите абсциссу точки касания.

Задача №9.
Прямая y=3x+4 является касательной к графику функции 3x^2-3x+c. Найдите c.

Задача №10.
Прямая y=-5x+8 является касательной к графику функции 28x^2+bx+15. Найдите b, учитывая, что абсцисса точки касания больше 0.