Муниципальное общеобразовательное автономное учреждение
«Средняя общеобразовательная школа № 40 с углублённым изучением математики имени В.М. Барбазюка» города Оренбурга
|
|
Согласовано ЗД по УВР ____________ / /
|
Принято методическим советом
Протокол № 1 от « » августа 2020 г. |
Утверждено Директор МОАУ «СОШ № 40» _________ /Кузнецова Р.Ш./
Приказ № 01- / от « » августа 2020г.
|
РАБОЧАЯ ПРОГРАММА
по геометрии
в 11 классе
Среднее общее образование
(профильный уровень)
2020-2021 учебный год
Составитель: Леотина И.В.
г. Оренбург,2020 год
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ КУРСА ОБУЧАЮЩИМИСЯ
В результате изучения математики на профильном уровне ученик 11 класса должен
знать/понимать:
• значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
• значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;
• идеи расширения числовых множеств как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
• значение идей, методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;
• возможности геометрии для описания свойств реальных предметов и их взаимного расположения;
• универсальный характер законов логики математических рассуждений, их применимость в различных областях человеческой деятельности;
• различие требований, предъявляемых к доказательствам в математике, естественных, социально-экономических и гуманитарных науках, на практике;
• роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;
• вероятностных характер различных процессов и закономерностей окружающего мира;
ГЕОМЕТРИЯ
Уметь:
• соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;
• изображать геометрические фигуры и тела, выполнять чертеж по условию задачи;
• решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;
• проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;
• вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;
• применять координатно-векторный метод для вычисления отношений, расстояний и углов;
• строить сечения многогранников и изображать сечения тел вращения;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
• исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
• вычисления длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.
СОДЕРЖАНИЕ КУРСА ГЕОМЕТРИИ 11 КЛАССА
Тела и поверхности вращения.
Цилиндр. Усеченный конус. Конус. Основание, высота, боковая поверхность, образующая, развертка.
Осевые сечения и сечения параллельные основанию.
Шар и сфера, их сечения.
Эллипс, гипербола, парабола как сечения конуса. Касательная плоскость к сфере. Сфера, вписанная в многогранник. Сфера, описанная около многогранника. Цилиндрические и конические поверхности.
Понятие об объёме тела. Отношение объёмов подобных тел. Объём прямоугольного параллелепипеда. Объём прямой призмы и цилиндра. Объём наклонной призмы, пирамиды и конуса. Формулы объема куба, параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы. Объём шара и площадь сферы.
Уравнения сферы.
Формула расстояния от точки до плоскости.
Векторы. Модуль вектора. Равенство векторов. Понятие вектора в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы. Разложение по трем некомпланарным векторам. Координаты и векторы.
Декартовы координаты в пространстве. Формула расстояния между двумя точками. Координаты точки и координаты вектора. Угол между векторами. Скалярное произведение векторов.
Календарно-тематическое планирование
|
Номер урока |
Название темы |
Количество часов |
Сроки |
|
|
По плану |
Фактическое проведение |
|||
|
1 |
Векторы. Модуль вектора. Равенство векторов. Понятие вектора в пространстве. |
1 |
|
|
|
2 |
Сложение и вычитание векторов. Умножение вектора на число. |
1 |
|
|
|
3 |
Сложение и вычитание векторов. Умножение вектора на число |
1 |
|
|
|
4 |
Компланарные векторы |
1 |
|
|
|
5 |
Компланарные векторы |
1 |
|
|
|
6 |
Входная контрольная работа |
1 |
|
|
|
7 |
Разложение по трем некомпланарным векторам |
1 |
|
|
|
8 |
Координаты и векторы. |
1 |
|
|
|
9 |
Декартовы координаты в пространстве |
1 |
|
|
|
10 |
Координаты точки и координаты вектора |
1 |
|
|
|
11 |
Координаты точки и координаты вектора |
1 |
|
|
|
12 |
Формула расстояния между двумя точками. |
1 |
|
|
|
13 |
Угол между векторами. |
1 |
|
|
|
14 |
Угол между векторами. Формула расстояния от точки до плоскости. |
1 |
|
|
|
15 |
Скалярное произведение векторов |
1 |
|
|
|
16 |
Скалярное произведение векторов |
1 |
|
|
|
17 |
Скалярное произведение векторов |
1 |
|
. |
|
18 |
Контрольная работа по теме «Векторы в пространстве. Метод координат в пространстве». |
1 |
|
|
|
19 |
Зачёт по теме «Векторы в пространстве. Метод координат в пространстве». |
1 |
|
|
|
20 |
Тела и поверхности вращения. Цилиндр |
1 |
|
|
|
21 |
Цилиндр |
1 |
|
|
|
22 |
Цилиндр. Формулы площади поверхностей цилиндра и конуса. |
1 |
|
|
|
23 |
Цилиндр |
1 |
|
|
|
24 |
Конус. Усеченный конус. Формулы площади поверхностей цилиндра и конуса. |
1 |
|
|
|
25 |
Конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. |
1 |
|
|
|
26 |
Конус. Основание, высота, боковая поверхность, образующая, развертка. Эллипс, гипербола, парабола как сечения конуса. |
1 |
|
|
|
27 |
Шар и сфера, их сечения. |
1 |
|
|
|
28 |
Шар и сфера, их сечения. Касательная плоскость к сфере. |
1 |
|
|
|
29 |
Контрольная работа за 1 полугодие |
1 |
|
|
|
30 |
Шар и сфера, их сечения. Уравнения сферы. Объём шара и площадь сферы |
1 |
|
|
|
31 |
Сфера, вписанная в многогранник. |
1 |
|
|
|
32 |
Сфера, описанная около многогранника. |
1 |
|
|
|
33 |
Цилиндрические и конические поверхности. |
1 |
|
|
|
34 |
Контрольная работа по теме «Цилиндр, конус, шар». |
1 |
|
|
|
35 |
Зачёт по теме «Цилиндр, конус, шар». |
1 |
|
|
|
36 |
Понятие об объёме тела. Объём прямоугольного параллелепипеда. Формулы объема куба, параллелепипеда, призмы, цилиндра. |
1 |
|
|
|
37 |
Объём прямоугольного параллелепипеда |
1 |
|
|
|
38 |
Объём прямой призмы и цилиндра |
1 |
|
|
|
39 |
Объём прямой призмы и цилиндра |
1 |
|
|
|
40 |
Объём прямой призмы и цилиндра |
1 |
|
|
|
41 |
Объём прямой призмы и цилиндра. Отношение объёмов подобных тел. |
1 |
|
|
|
42 |
Объём наклонной призмы, пирамиды и конуса. Формулы объема пирамиды и конуса. |
1 |
|
|
|
43 |
Объём наклонной призмы, пирамиды и конуса |
1 |
|
|
|
44 |
Объём наклонной призмы, пирамиды и конуса |
1 |
|
|
|
45 |
Объём шара и площадь сферы. Формулы объема шара и площади сферы. |
1 |
|
|
|
46 |
Объём шара и площадь сферы. Формулы объема шара и площади сферы. |
1 |
|
|
|
47 |
Объём шара и площадь сферы. Формулы объема шара и площади сферы. |
1 |
|
|
|
48 |
Объём шара и площадь сферы. Формулы объема шара и площади сферы. |
1 |
|
|
|
49 |
Контрольная работа по теме «Объёмы тел». |
1 |
|
|
|
50 |
Зачёт по теме «Объёмы тел». |
1 |
|
|
|
51 |
Итоговое повторение |
1 |
|
|
|
52 |
Итоговое повторение |
1 |
|
|
|
53 |
Итоговое повторение |
1 |
|
|
|
54 |
Итоговое повторение |
1 |
|
|
|
55 |
Итоговое повторение |
1 |
|
|
|
56 |
Итоговое повторение |
1 |
|
|
|
57 |
Итоговое повторение |
1 |
|
|
|
58 |
Итоговое повторение |
1 |
|
|
|
59 |
Итоговое повторение |
1 |
|
|
|
60 |
Контрольная работа за год |
1 |
|
|
|
61 |
Итоговое повторение |
1 |
|
|
|
62 |
Итоговое повторение |
1 |
|
|
|
63 |
Итоговое повторение |
1 |
|
|
|
64 |
Итоговое повторение |
1 |
|
|
|
65 |
Итоговое повторение |
1 |
|
|
|
66 |
Итоговое повторение |
1 |
|
|
|
67 |
Итоговое повторение |
1 |
|
|
|
68 |
Итоговое повторение |
1 |
|
|
Оценочные материалы
Контрольная работа по теме «Векторы в пространстве. Метод координат в пространстве»
Вариант I
ЧАСТЬ 1
1.Дан куб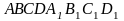 
. Найдите угол между векторами 
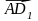и 
.
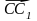А) Найдите значение т, при котором векторы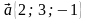 
и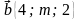 
перпендикулярны.
Б) Найдите угол между прямыми AB и СD, есл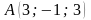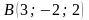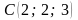и 
, 
, 
и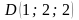 
.
2. Вычислите скалярное произведение векторов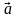 
и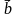 
, если 
, 
.
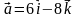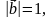
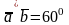3. Даны векторы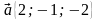 
и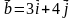 
. Найдите 
.
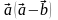ЧАСТЬ 2
1. Даны векторы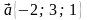 
и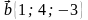 
. Определите, при каких значениях 
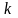угол между векторам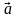и и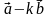 
тупой.
2. В кубе ABCDA1B1C1D1, точка M – середина ребра DD1. Используя метод координат, найдите угол между прямыми BМ и AD1.
Вариант II
ЧАСТЬ 1
1. Дан куб 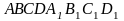. Найдите угол между векторам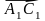и 
и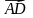 
.
А) Найдите значение т, при котором векторы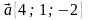 
и 
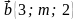перпендикулярны.
Б) Найдите угол между прямыми AB и СD, есл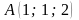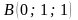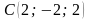и 
, 
, 
и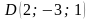 
.
2. Вычислите скалярное произведение векторов 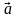и 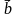, если 
, 
.
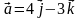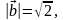
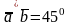3. Даны векторы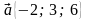 
и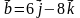 
. Найдите 
.
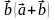ЧАСТЬ 2
1.Даны векторы 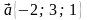и 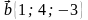. Определите, при каких значениях 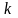угол между векторам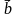и и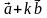 
острый.
2. В кубе ABCDA1B1C1D1, точкаО – центр грани ABCD. Используя метод координат, найдите угол между прямыми BО и A1D.
Контрольная работа по теме «Цилиндр, конус, шар»
Вариант I
1. Радиус основания цилиндра равен 5 см, а высота цилиндра равна 6 см. Найдите площадь сечения, проведенного параллельно оси цилиндра на расстоянии 4 см от нее.
2. Радиус шара равен 17 см. Найдите площадь сечения шара, удаленного от его центра на 15 см.
3. Образующая конуса l наклонена к плоскости основания под углом в 300. Найдите высоту конуса и площадь осевого сечения.
4. Осевое сечение цилиндра – квадрат, диагональ которого 4 см. Найдите площадь боковой поверхности цилиндра.
5. Площадь сечения шара плоскостью, проведенной через конец диаметра под углом 300 к нему, равна 75π см2. Найдите диаметр шара.
Вариант II
1. Высота цилиндра равна 8 см, а радиус цилиндра равен 5 см. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра.
2. Радиус сферы равен 15 см. Найдите длину окружности сечения, удаленного от центра сферы на 12 см.
3. Радиус основания конуса равен 3 м, а высота 4 м. Найдите образующую и площадь осевого сечения.
4. Осевое сечение цилиндра – квадрат, площадь основания цилиндра равна 16π см2. Найдите площадь боковой поверхности цилиндра.
5. Диаметр шара равен d. Через конец диаметра проведена плоскость под углом 450 к нему. Найдите площадь сечения шара этой плоскостью.
Контрольная работа по теме «Объёмы тел»
Вариант I
1. Боковое ребро правильной треугольной пирамиды равно 6 см и составляет с плоскостью основания угол 600. Найдите объем пирамиды.
2. Диаметр шара равен высоте конуса, образующая которого составляет с плоскостью основания угол в 600. Найдите отношение объемов конуса и шара.
3. Объем цилиндра равен 96π см3, площадь его осевого сечения 48π см2. Найдите площадь сферы, описанной около цилиндра.
4. В конус вписана пирамида. Основанием пирамиды служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 300. Боковая грань пирамиды, проходящая через данный катет, составляет с плоскостью основания угол в 450. Найдите объем конуса.
Вариант II
1. Апофема правильной треугольной пирамиды равно 4 см, а двугранный угол при основании равен 600. Найдите объем пирамиды.
2. Диаметр шара равен высоте цилиндра, осевое сечение которого квадрат. Найдите отношение объемов цилиндра и шара.
3. В конус, осевое сечение которого есть правильный треугольник, вписан шар. Объем конуса равен 40π см3, площадь сечения 30π см2. Найдите площадь сферы.
4. В цилиндр вписана призма. Основанием призмы служит прямоугольный треугольник, катет которого равен 2а, а прилежащий угол равен 300. Диагональ большей боковой грани призмы составляет с плоскостью основания угол в 450. Найдите объем цилиндра.
Зачёт по теме «Векторы в пространстве. Метод координат в пространстве»
Вариант 1
1. Даны точки А(5; 0; 2), В(4; -3; 2),
С(0; 0; 1), D(2; -4; -4). Найдите:
а) координаты векторов АВ и СD;
б) координаты векторов а = АВ + СD,
b = AB – CD, с = -⅓АВ;
в) длины векторов а и b;
г) скалярное произведение векторов
АВ и СD, а и b.
2. Вершины треугольника КМN имеют координаты K(-2; 3; -2), M(8; 1;2), N(2; -3; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой
Вариант 2
1.Даны точки А(5; -5; 0), В(-2; 1; -3),
С(0; 3; 1), D(1; 3; -4). Найдите:
а) координаты векторов АВ и СD;
б) координаты векторов а = АВ + СD,
b = AB – CD, с = ⅓АВ;
в) длины векторов а и b;
г) скалярное произведение векторов
АВ и СD, а и b.
2. Вершины треугольника КМN имеют координаты K(8; 3; 5), M(14; 1;0), N(12; -5; 0). Найдите:
а) координаты середины стороны КМ;
б) длины сторон треугольника и определите вид этого треугольника (равносторонний, равнобедренный или разносторонний);
в) вычислите косинус угла М и определите вид этого угла (острый, прямой или тупой).
Зачёт по теме «Цилиндр, конус, шар»
1.Сформулируйте определение цилиндра, его элементов (основания, ось, образующая, боковая поверхность, высота, радиус основания). Осевое сечение цилиндра и сечение цилиндра плоскостью, параллельной основаниям. Площадь поверхности цилиндра (с объяснением).
2. .Сформулируйте определение конуса, его элементов (основание, образующая, ось, боковая поверхность, высота, радиус основания). Осевое сечение конуса и сечение конуса плоскостью, параллельной основанию. Площадь поверхности конуса (с выводом).
3. .Сформулируйте определение усеченного конуса, его элементов (основания, образующая, ось, боковая поверхность, высота, радиус основания). Осевое сечение усеченного конуса и сечение усеченного конуса плоскостью, параллельной основаниям. Площадь поверхности усеченного конуса.
4. Сформулируйте определение сферы и шара, его элементов (центр, радиус, диаметр). Сечения шара. Уравнение сферы.
5. Сформулируйте определение касательной плоскости к сфере. Докажите свойство касательной плоскости.
6. Сформулируйте определение сферы и шара, его элементов (центр, радиус, диаметр). Расскажите о взаимном расположении сферы и плоскости.
7. Высота конуса равна 10 см, угол между высотой и образующей конуса равен 45 . Найдите площадь сечения конуса плоскостью, проведенной через две образующие, угол между которыми 30
.
8. Радиус шара равен 12 см. Через конец радиуса проведена плоскость под углом 45 к нему. Найдите площадь сечения.
9. Сечение цилиндра плоскостью, параллельной оси, отсекает от окружности основания дугу в 120 . Найдите площадь сечения, если высота цилиндра равна 7 см, а расстояние между осью цилиндра и секущей плоскостью равно 2 см.
10, Диагональ осевого сечения равностороннего цилиндра равна 8 см. Найдите площадь его основания.
11. Радиусы оснований усеченного конуса 6 и 2 см, образующая наклонена к основанию под углом 60 . Найдите высоту и образующую конуса.
12. Каждое ребро правильной треугольной призмы равно a Найдите площадь осевого сечения вписанного цилиндра.
13. Радиус шара равен R. Найдите площадь диагонального сечения вписанного куба.
14. Ребро куба равно a. Найдите площадь осевого сечения описанного цилиндра.
15. Образующая конуса равна 13 см. В конус вписана пирамида, основанием которой служит прямоугольный треугольник с катетами 6 и 8 см. Найдите высоту пирамиды.
16. Образующая конуса равна 4 см и наклонена к плоскости основания под углом 60 . Найдите боковую поверхность вписанной в конус правильной треугольной пирамиды.
17. Площадь осевого сечения равностороннего цилиндра (диаметр равен образующей) равна 16 см2. Найдите боковую поверхность вписанной в цилиндр правильной шестиугольной призмы.
18. Через вершину конуса и хорду основания, стягивающую дугу в 60 , проведено сечение, составляющее с плоскостью основания угол в
45 . Найдите площадь сечения, если радиус основания равен 4 см.
Зачёт по теме «Объёмы тел»
1 вариант
1. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
2. Найдите объем прямой призмы, в основании которой лежит параллелограмм со сторонами 6,7 см и 8 см, угол между этими сторонами равен 300, а высота призмы равна 10 см.
3. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
4. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем конуса, если объем цилиндра равен 36.
5. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 22 раза?
6. Найдите объем пирамиды, высота которой равна 5, а основание — прямоугольник со сторонами 7 и 6.
7. В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 18 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в
.
8. Площадь большого круга шара равна 9. Найдите площадь поверхности шара.
2 вариант
1. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
2. Найдите объем прямой призмы, в основании которой лежит трапеция с основаниями 6,8 см и 4,12 см и высотой 7 см, а высота призмы равна 5 см.
3. Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите .
4. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем конуса, если объем цилиндра равен 27.
5. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 6 раз?
6. Найдите объем пирамиды, высота которой равна 1, а основание — прямоугольник со сторонами 4 и 3.
7. В цилиндрический сосуд налили воды. Уровень жидкости оказался равным 25 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 5 см. Чему равен объем детали? Ответ выразите в
.
8. Площадь большого круга шара равна 39. Найдите площадь поверхности шара.
Нормы оценок письменных работ по математике
Единые нормы являются основой при оценке как контрольных, так и всех других письменных работ по математике. Они обеспечивают единство требований к обучающимся со стороны всех учителей образовательного учреждения. Применяя эти нормы, учитель должен индивидуально подходить к оценке каждой письменной работы учащегося, обращать внимание на качество выполнения работы в целом, а затем уже на количество ошибок и на их характер.
Ошибка, повторяющаяся в одной работе несколько раз, рассматривается, как одна ошибка;
За орфографические ошибки оценка не снижается. Однако ошибки в написании математических терминов, уже встречающихся школьникам класса, должны учитываться как недочеты в работе.
При оценке письменных работ по математике различают:
Грубые ошибки
Ошибки
Недочеты
К грубым относятся ошибки в вычислениях, свидетельствующие о незнании таблицы умножения и сложения, связанные с незнанием алгоритма письменного сложения и вычитания, умножения и деления на одно – или двузначное число и т.п., и явном неумении применять, о незнании приемов решения задач, аналогичных ранее изученным. Если грубая ошибка встречается в работе только в одном случае из нескольких аналогичных, то при оценке работы эта ошибка может быть приравнена к негрубой.
Негрубые ошибки: ошибки, связанные с недостаточно полным усвоением текущего учебного материала, не вполне точно сформулированный вопрос или пояснение при решении задачи, неточности при выполнении геометрических построений и т.п.
Недочетами считаются нерациональные записи при вычислениях, нерациональные приемы вычислений, преобразований и решений задач, небрежное выполнение чертежей и схем, отдельные погрешности в формулировке пояснения или ответа в задаче, неполное сокращение дробей или членов отношения, обращение смешанных чисел в неправильную дробь при сложении и вычитании, пропуск наименований, перестановка цифр при записи чисел, ошибки, допущенные при переписывании.
2. Оценка письменной работы по выполнению вычислительных заданий и
алгебраических преобразований.
Оценка «5» ставится за безукоризненное выполнение письменной работы, т.е.:
а) если решение всех примеров верное;
б) если все действия и преобразования выполнены правильно, без ошибок; все записи хода решения расположены последовательно, а так же сделана проверка решения в тех случаях, когда это требуется.
Оценка «4»ставится за работу, в которой допущена одна ошибка негрубая или два-три недочета.
Оценка «3»ставится в следующих случаях:
а) если в работе иметься одна грубая ошибка и не более одной негрубой ошибки;
б) при наличии одной грубой ошибки и одного – двух недочетов;
в) при отсутствии грубых ошибок, но при наличии от двух до четырех негрубых ошибок;
г) при наличии двух негрубых ошибок не более трех недочетов;
д) при отсутствии ошибок, но при наличии четырех недочетов и более недочетов;
е) если неверно выполнено не более половины объема всей работы.
Оценка «2» ставиться, когда число ошибок превосходит норму, при которой может быть выставлена положительная оценка, или если неправильно выполнено менее половины всей работы.
Оценка «1» ставится, если ученик совсем не выполнил работу.
Примечание: Оценка «5» может быть поставлена, несмотря на наличие одного – двух недочетов, если ученик дал оригинальное решение заданий.
3.Оценка письменной работы на решение текстовых задач
Оценка «5»ставиться в том случае, когда задача решена правильно: ход решения задачи верен, все действия и преобразования выполнены, верно и рационально; в задаче, решаемой с вопросами или пояснениями к действиям, даны точные и правильные формулировки; в задаче, решаемой с помощью уравнения, даны необходимые пояснения; записи правильны, расположены последовательно, дан верный исчерпывающий ответ на вопросы задачи; сделана проверка решения.
Оценка «4»ставиться в том случае, если при правильном ходе решения задачи допущена одна негрубая ошибка или два – три недочета.
Оценка «3»ставиться в том случае, если ход решения правилен, но допущены:
. Одна грубая ошибка и не более одной не грубой;
. Одна грубая ошибка и не более двух недочетов;
. Три – четыре негрубые ошибки при отсутствии недочетов;
. Допущено не более двух негрубых ошибок и трех недочетов;
. Более трех недочетов при отсутствии ошибок.
Оценка «2»ставиться в том случае, если число ошибок превосходит норму, при которой быть может выставлена положительная оценка.
Оценка «1»ставиться в том случае, если ученик не выполнил ни одного задания.
4.Оценка комбинированных письменных работ по математике
Письменная работа, подлежащая оцениванию, может состоять из задач и примеров. В таком случае преподаватель сначала дает предварительную оценку каждой части работы, а затем общую, руководствуясь следующим:
Если обе части работы оценены одинаково, то эта оценка должна быть общей для всей работы в целом;
. Если оценки частей разнятся на один балл, то за работу в целом, как правило, ставиться балл, оценивающий основную часть работы;
Если одна часть работы оценена баллом «5», а другая – баллом «3», то преподаватель может оценить такую работу в целом баллом «4» при условии, что оценка «5» поставлена за основную часть работы;
Если одна из частей работы оценена баллом «5» или «4», а другая – баллом «2» или «1», то преподаватель может оценить всю работу баллом «3» при условии, что высшая из двух данных оценок поставлена за основную часть работы.
5. Оценка текущих письменных работ
При оценке повседневных обучающих работ по математике учитель руководствуется указанными нормами оценок, но учитывает степень самостоятельности выполнения работ учащимися.
Обучающие письменные работы, выполненные учащимися вполне самостоятельно с применением ранее изученных и хорошо закрепленных знаний, оцениваются так же, как и контрольные работы.
Обучающие письменные работы, выполненные вполне самостоятельно, на только что изученные и недостаточно закрепленные правила, могут оцениваться менее строго.
Письменные работы, выполненные в классе с предварительным разбором их под руководством учителя, оцениваются более строго.
Домашние письменные работы оцениваются так же, как классные работы обучающего характера.
