
Теорема Пифагора

Содержание
- О Пифагоре.
- Из истории теоремы.
- Доказательство теоремы.
- Закрепление материала.
- Решение старинных задач.

Что известно о Пифагоре
- В VI веке до н.э. в Древней Греции жил ученый Пифагор родом из Самоса.
- В молодости он много путешествовал по странам Востока, побывал в Египте и Вавилоне, где изучал разные науки, в том числе математику .
- Вернувшись на родину, Пифагор основал философскую школу закрытого типа- Пифагорейский союз . Каждый вступающий в него отрекался от имущества и давал клятву хранить в тайне учение основателя.
- Пифагорейцы занимались математикой, философией , естественными науками. Ими были сделаны важные открытия в арифметике и геометрии.
- В школе существовало правило , по которому авторство работ присваивалось Пифагору . Так что неизвестно , какие открытия принадлежат самому учёному.

Из истории теоремы
- « Площадь квадрата , построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах », или в виде задачи: «Доказать, что квадрат , построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов , построенных на катетах : S=S 1 +S 2 » — так формулировали теорему во времена Пифагора
S
S 1
S 2

Из истории теоремы
Долгое время считалось , что до Пифагора эта теорема не была известна.
В настоящее время установлено, что она встречается в вавилонских текстах, написанных за 1200 лет до Пифагора! Вероятно тогда теорема ещё не была доказана, а соотношение между катетами и гипотенузой было получено опытным путём.
Была она известна и древним китайцам, и индусам.
Таким образом, Пифагор не открыл замечательное свойство прямоугольного треугольника, но, вероятно, первым обобщил и доказал его , перенеся таким самым из области практики в область науки. К сожалению, сведения о доказательстве до нес не дошли.

Из истории теоремы
- Сегодня известно более ста различных доказательств теоремы Пифагора
- Вероятно соотношение между катетами и гипотенузой первоначально было установлено для равнобедренного прямоугольного треугольника .
а
b
c
- По рисунку видим, что квадрат , построенный на его гипотенузе , разбивается диагоналями на четыре равных треугольника , а квадраты , построенные на катетах , содержат по два таких же треугольника . Замечаем, что площадь большого квадрата равна сумме площадей малых квадратов

Из истории теоремы
- Учащиеся средних веков считали доказательство теоремы очень трудным и прозвали его «ослиным мостом» или «бегством убогих», так как слабые ученики бежали от геометрии, а те, кто заучивал теоремы наизусть , без понимания, были не в состоянии осилить теорему Пифагора: она служила для них чем-то вроде непреодолимого моста.
- Из-за иллюстрирующих теорему чертежей учащиеся называли её также «ветряной мельницей», рисовали забавные карикатуры и придумывали стишки:
- «Пифагоровы штаны
Во все стороны равны»

Из истории теоремы
- Теорема Пифагора занимает в геометрии особое место.
- На её основе можно вывести или доказать большинство теорем.
- А ещё она замечательна тем, что сама по себе вовсе не очевидна .
- Сколько не рассматривай прямоугольный треугольник, никак не увидишь, что его стороны а, b , с связывает простое соотношение
с
а
b
а ² + b ²= с²

Доказательство теоремы
- Доказательство: рассмотрим прямоугольный треугольник с катетами а, b и гипотенузой с .
- Докажем, что
- Достроим треугольник до квадрата со стороной а+ b
b
c
а
с 2 =a 2 +b 2
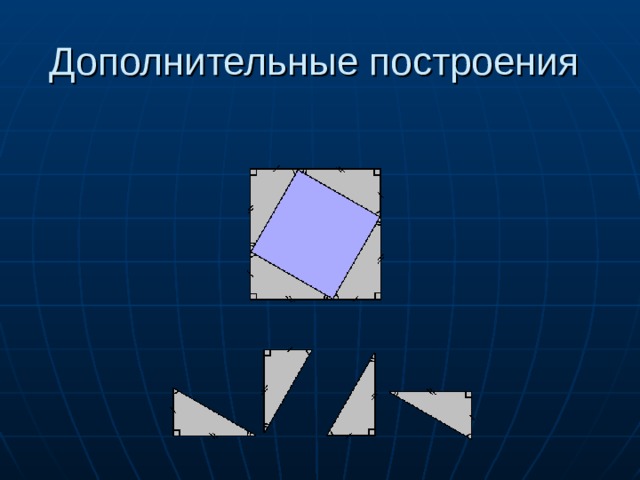
Дополнительные построения
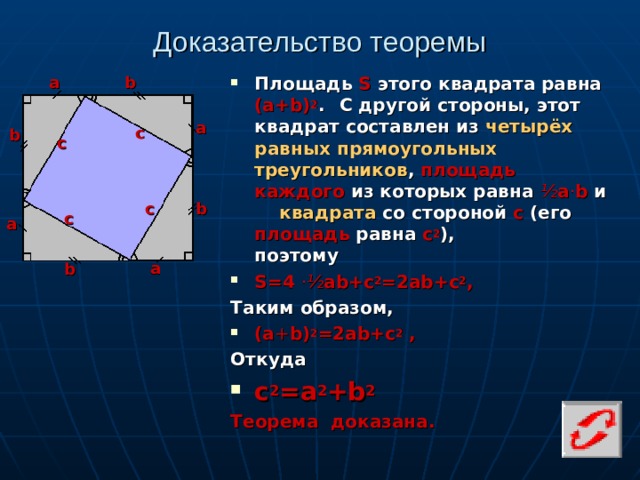
Доказательство теоремы
b
а
- Площадь S этого квадрата равна (а+ b ) 2 . С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников , площадь каждого из которых равна ½ а · b и квадрата со стороной с (его площадь равна с 2 ), поэтому
- S =4 · ½ а b +с 2 =2а b +с 2 ,
Таким образом,
- (а + b ) 2 =2а b +с 2 ,
Откуда
- с 2 =a 2 +b 2
Теорема доказана.
а
с
b
с
b
с
с
а
а
b
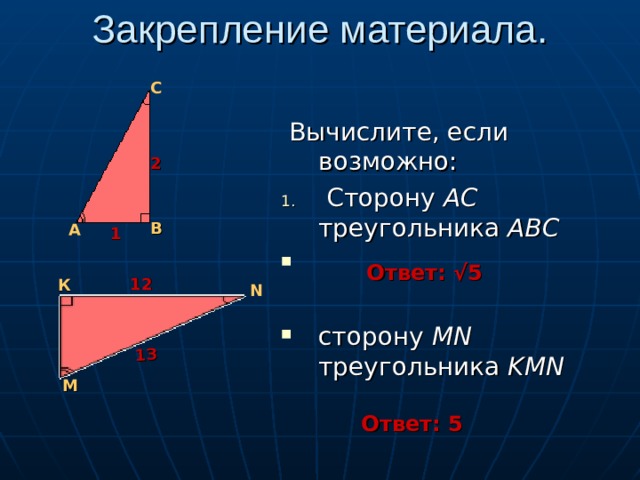
Закрепление материала.
13
С
Вычислите, если возможно:
- Сторону АС треугольника АВС
- сторону MN треугольника KMN
2
В
А
1
Ответ: √5
12
К
N
М
Ответ: 5
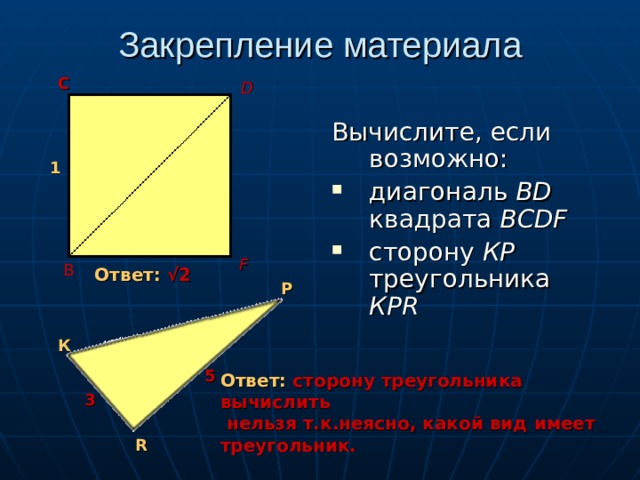
Закрепление материала
С
D
Вычислите, если возможно:
- диагональ ВD квадрата BCDF
- сторону КР треугольника КР R
1
F
В
Ответ: √2
Р
К
5
Ответ: сторону треугольника вычислить
нельзя т.к.неясно, какой вид имеет треугольник.
3
R
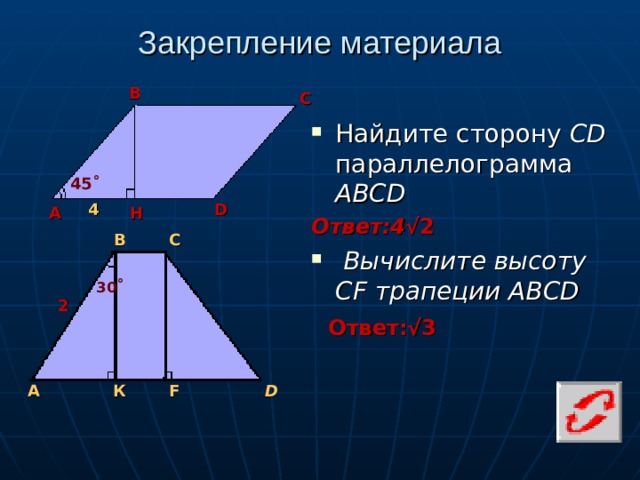
Закрепление материала
В
С
- Найдите сторону CD параллелограмма АВСD
Ответ:4 √2
- Вычислите высоту CF трапеции ABCD
45˚
4
D
Н
А
В
С
30 ˚
2
Ответ:√3
А
К
F
D

Задача из «Арифметики» Л.Ф.Магницкого.
- Случися некоему человеку к стене лествицу прибрати, стены же тоя высота есть 117 стоп. И обрете лествицу долготою 125 стоп. И ведати хощет, колико стоп сея лествицы нижний конец от стены omcmoятu имать .

Решение
- Р е ш е н и e. Треугольник АВС — прямоугольный
- Пусть ВС = х стоп, тогда по теореме Пифaгopa АС 2 + СВ 2 =АВ 2 ,
- 117 2 + x 2 = 125 2 ;
- х 2 = 125 2 — 117 2 ,
- х 2 = (125- 117)(125 + 117),
- х 2 =8 · 242, х =44.
- О т в е т: 44 стопы
А
117
125
С
В

Задача Бхаскары (индийского математика XII в.)
- На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал… Бедный тополь упал. И угол прямой C теченьем реки его ствол составлял. Запомни теперь, что в том месте река В четыре лишь фута была широка. Верхушка склонилась у края реки, Осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: У тополя как велика высота
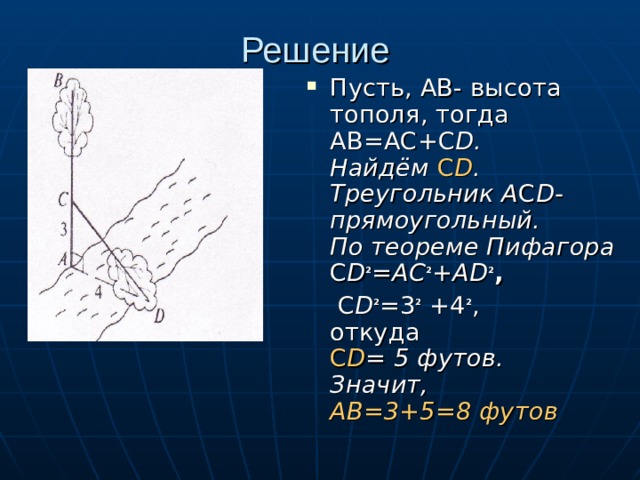
Решение
- Пусть, АВ- высота тополя, тогда АВ=АС+С D. Найдём С D . Треугольник А С D- прямоугольный. По теореме Пифагора С D ² =АС ² +АD ² ,
С D ² =3 ² +4 ² , откуда С D = 5 футов. Значит, АВ=3+5=8 футов

Из древнеиндийского трактата
- Над озером тихим, C полфута размером, высился лотоса цвет. Он рос одиноко. И ветер порывом Отнес его в сторону. Нет боле цветка над водой. Нашёл же рыбак его ранней весной B двух футах от места, где рос. Итак, предложу я вопрос: Как озера вода здесь глубока?
½
2
С
В
А
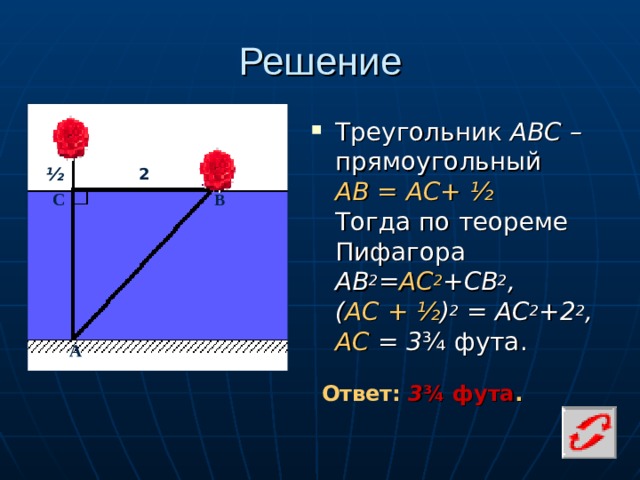
Решение
- Треугольник АВС – прямоугольный АВ = АС+ ½ Тогда по теореме Пифагора AB 2 = AC 2 +CB 2 , ( АС + ½ ) 2 = АС 2 +2 2 , АС = 3 ¾ фута.
½
2
С
В
А
Ответ: 3 ¾ фута .