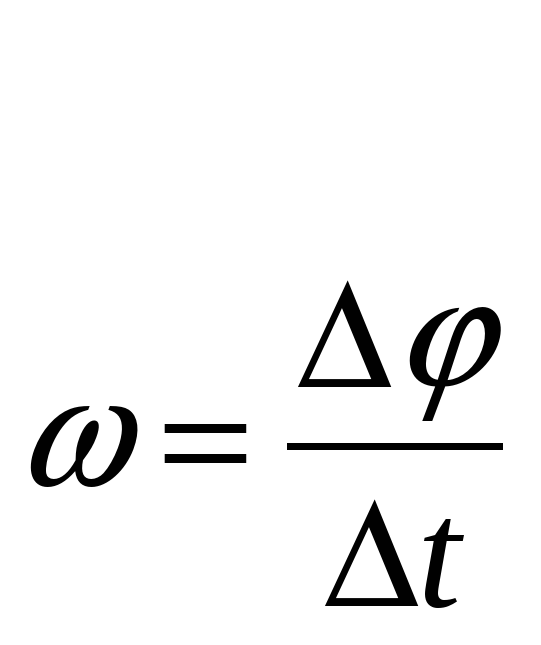Интегрированный урок по физике и математике «Производная как механизм изучения социальных и природных явлений»

Интегрированный урок по физике и математике «Производная как механизм изучения социальных и природных явлений»

Урок проводился в 11 классе учителями физики и математики.

Продолжительность урока 45 минут.

Это урок систематизации знаний, на котором расширяются и углубляются знания учащихся, полученные на предыдущих уроках

Учителя:

Ершова Анна Александровна, учитель физики высшей категории;
Горина Татьяна Евгеньевна, учитель математики высшей категории.

Цель урока: углубление знаний учащихся о моделировании процессов действительности с помощью аппарата производной.

сформировать у учащихся умение решать простейшие практические задачи с использованием методов дифференциального исчисления.

Задачи урока:

• продолжить формировать умения устанавливать связь между предметами и применять полученные знания по математике при решении практических задач;

• развивать логическое мышление, умение анализировать, делать выводы;

• развивать познавательный интерес у учащихся через раскрытие практической необходимости и теоретической значимости связи между предметами.

Учебные:

— Закрепить понятие физического и геометрического смысла производной.
— Показать межпредметную связь на примере математического моделирования.
— Научить применять полученную модель на практике.

Воспитательные:

— Обучение навыкам: планирования деятельности, работы в оптимальном темпе, подведения итогов.
— Развитие умения оценивать свои способности, свое положение в группе, контактировать с товарищами.
— Вызвать чувства ответственности и сопереживания.

Развивающие:

— Обучение навыкам работы с компьютером.

— Развитие умения находить нужную литературу, выполнять и оформлять научно-исследовательскую работу.
— Формирование «ключевых компетенций».

Тип занятия:

-по основной дидактической цели: совершенствование знаний, умений, навыков;

и частично, контроля знаний.
-по способу проведения: интегрированное занятие.

Оборудование: экран, проектор, творческие работы учащихся (презентации, буклет,), бейджики

Ход урока

1. Организационный момент.

Учитель математики: Здравствуйте

Учитель физики: Добрый день

Эпиграф урока «Без математики нельзя понимать ни основ современной техники, ни того, как ученые изучают природные и социальные явления»

…Нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…

Н.И. Лобачевский

Обсуждение темы занятия.

Учитель математики: Ребята, выясним ключевое слово урока:

1. С ее появлением математика перешагнула из алгебры в математический анализ;

2. Ньютон назвал ее «флюксией» и обозначал точкой;

3. Бывает первой, второй …

4. Обозначается штрихом

Итак, сегодня на уроке мы поговорим о производной, о ее применении.

Всем известно высказывание «Мал золотник да дорог». Одним из таких «золотников» в математике является производная. Производная применяется при решении задач математики, физики, химии, биологии, географии, экономики и других дисциплин. Она позволяет решать задачи просто, красиво, интересно.

Тема нашего урока: «Производная как механизм изучения социальных и природных явлений».

1. Проверка домашнего задания.

Учитель математики: На предыдущем уроке было предложено задание по истории возникновения производной. Кто может рассказать?

Выступление учащегося (используется слайд презентации «История производной»)

1. Повторение.

Учитель математики: Прежде чем приступить к повторению основных направлений применения производной, проверим нашу готовность к вычислению производных. Учащиеся работают в группах на ноутбуках. Проверка по слайду на презентации.

Установите соответствие между функциями и соответствующими им производными

Ключ для проверки:

Учитель физики:

— Понятие производной так и осталось бы математически абстрактным символом, если бы не уроки физики.

— Назовите физические величины, являющиеся производной по времени от других физических величин, и напишите их обозначения в столбик (Повторение физических формул. Работа с таблицей (она изначально помещена на доске, но заполнен только первый столбец).

Учитель физики: На практике во многих отраслях науки используется обобщение равенства. Если некий процесс протекает по закону S=S(t), то S’(t) – скорость протекания этого процесса в момент времени t.

1. Решение задач.

Учитель математики: Применим наши теоретические знания на практике и покажем ее применение в различных областях знаний.

Работа в группах. Каждая группа получает задачу определённого направления для применения производной, Учащиеся обсуждают ход решения, записывают решение. Проверка с помощью презентации.

1 группа «Социологи»

Задача. Командиру межгалактического космического корабля, движущемуся по закону , сообщили о том, что приборы зафиксировали неопознанный летающий объект, стремительно приближающийся к кораблю. Чтобы избежать столкновения, необходимо максимально увеличить скорость. Каким должно быть ускорение корабля в момент, когда скорость станет максимальной?

Решение.

, при t = 1 скорость максимальна,

a(1) = 0.

Ответ: 0

2 группа «Экономисты»

Задача. Потребление электроэнергии предприятиями и населением города с 8 ч до 18 ч описывается формулой , где , где — время в часах. В какой момент времени потребление энергии будет наибольшим?

Р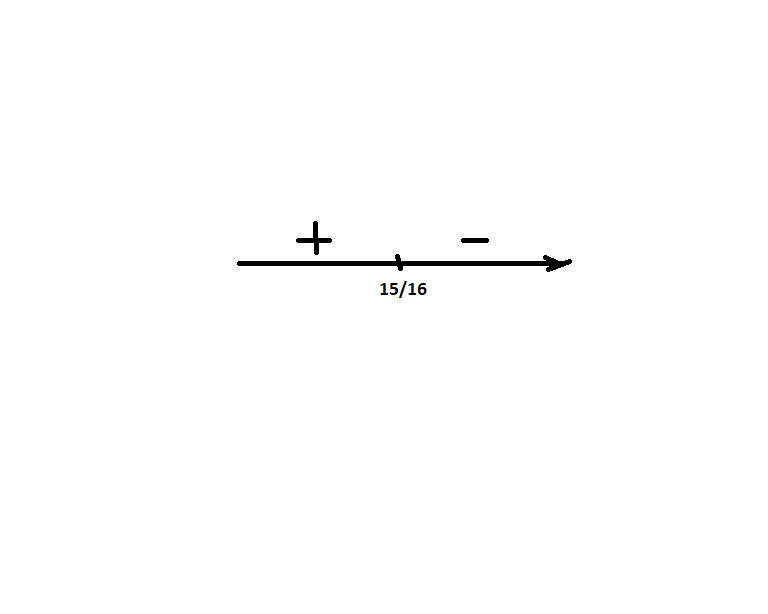ешение. _{ешение. ,}

-16t +15 = 0,

t = .

В точке t = функция имеет локальный максимум, значит, достигает наибольшего значения. Так как функция имеет локальный максимум, значит, достигает наибольшего значения. Так как , то примерно в 9 ч. потребление электроэнергии будет наибольшим.

3 группа «Биологи»

Задача. Количество зеленой массы растений в регионе изменяется по закону , где t — время в годах. Через сколько лет прирост зеленой массы растений будет наименьшим.

Решение.

.

2t – 500 = 0.

t = 250. — +

250

Итак, при t = 250 функция достигает локального минимума, значит, в этой точке принимает наименьшее значение.

Ответ: через 250 лет прирост зелёной массы будет наименьший.

4 группа «Инженеры»

Задача. Под каким углом надо сделать въезд на мост, если его высота 10 м, пролёт 120 м ?

Р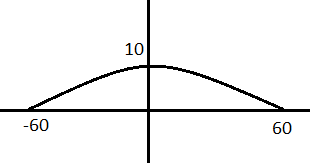ешение. Необходимо ввести прямоугольную систему координат и рассмотреть график функции _{ешение. Необходимо ввести прямоугольную систему координат и рассмотреть график функции . Графиком является парабола, ветви направлены вниз; b = 10. Найдём значение коэффициента a, подставив в формулу координаты точки (60; 0)}

Функция примет вид:

; .

Ответ:

Проверка решения задач, используя презентацию.

1. Группа «Физики»

Поплавковый акселерометр – это прибор позволяющий определить направление ускорения и его числовое значение.

Поплавкового акселерометра изготовлен следующим образом. На дно прозрачного пластикового сосуда с плоскопараллельными стенками и герметично завинчивающейся крышкой положили груз такой массы и формы, чтобы при ускоренных движениях он не перемещался по дну. Через отверстие в грузе пропустили черную нить, к концу которой прикрепили рыболовный поплавок. Получившийся поплавковый маятник расположили посередине сосуда и как можно ближе к его передней или задней стенке, чтобы уменьшить ошибку на параллакс. На соответствующую стенку сосуда липкой лентой наклеили шкалу так, чтобы ее верхний край находился на 9,8 см выше места крепления нити к грузу. Тогда, сантиметровые горизонтальные деления на шкале будут соответствовать ускорениям, кратным 1 м/с². Сосуд заполнили водой так, чтобы не осталось воздушных пузырьков. Готовый акселерометр закрепили на движущейся тележке.

Экспериментальная установка состоит из направляющей, вдоль которой движется акселерометр на тележке, и двух пружин, прикрепленных к ней и стойкам.

Задание. Определить с помощью поплавкового акселерометра направление ускорения и его числовое значение.

Выполнение практического задания.

1. Выведем прибор из положения равновесия. Переместим тележку влево и определим амплитуду колебаний. Она равна _________ см, выразим эту величину в метрах — ________ м.

2. С помощью секундомера определили период колебаний. Он равен _________ с.

3. Составим уравнение колебания тележки. При гармонических колебаниях смещение x тела изменяется по закону,

   где и ω =и ω = — амплитуда смещения и циклическая частота колебаний. Скорость – это производная координаты по времени:

1. При этом ускорение колеблющегося тела также колеблется по гармоническому закону — есть производная скорости по времени,
   причем оно противофазно смещению тела.

1. Вычислим ускорение при t= с

t , a=_______________________________________м/с²

Вывод: 1. В демонстрации гармонических колебаний акселерометра наблюдали, что указатель акселерометра всегда отклоняется в противополож­ную его смещению сторону, совершая колебание с той же часто­той, что и сам прибор, но в противофазе с ним.

2. Ускорение равно а = ___ м/с²

1. Подведение итогов.

Учитель математики:

— На экране представлены графики зависимости уровня ваших знаний от времени, в интервале от начала урока до его завершения. Пожалуйста, выберите тот график, который, на ваш взгляд, наиболее близок вам, принимая во внимание их разный характер.

— Имеют ли они отношение к теме нашего урока?

— Можно ли по этим графикам судить о скорости приращения ваших знаний в ходе урока?

— Всё, что было в физике темным и неясным, математика сделала правильным и очевидным.

Домашнее задание:

1. Составить и решить 2 задачи на применение производной.

2. Составить тест для проверки знаний по теме “Применение производной в физике”(10 класс) в компьютерном варианте.

Оценочный лист

Группа _________________________

Фамилия имя учащегося: _______________________________________