Квадратные уравнения
Урок обобщения и систематизации знаний
8 класс
0; D ? Как называется квадратное уравнение, у которого первый коэффициент – равен 1? Что значит решить уравнение?» width=»640″
- Равенство с переменной …..
- Уравнение второй степени…..
- От чего зависит количество корней квадратного уравнения?
- Сколько корней имеет квадратное уравнение, если D 0; D ?
- Как называется квадратное уравнение, у которого первый коэффициент – равен 1?
- Что значит решить уравнение?
Какое из выражений является квадратным уравнением?
- 3х + 1 = 0;
- г) 5х² — х — 4 = 0;
б) 5х – 4х ² = 0;
д) 4х – 8 = 0;
в) 4х² + 5х + 3;
е) 4х – 2х² = 20 .
Каждому уравнению
соотнесите его вид:
НЕПОЛНОЕ ПОЛНОЕ
5х 2 – 9х — 2 = 0
х 2 – 9х + 20 = 0
х 2 – 7х = 0
х 2 – 49 = 0
1,6х 2 – 2х — 5 = 0
х 2 = 50
х 2 + 8х + 12 = 0
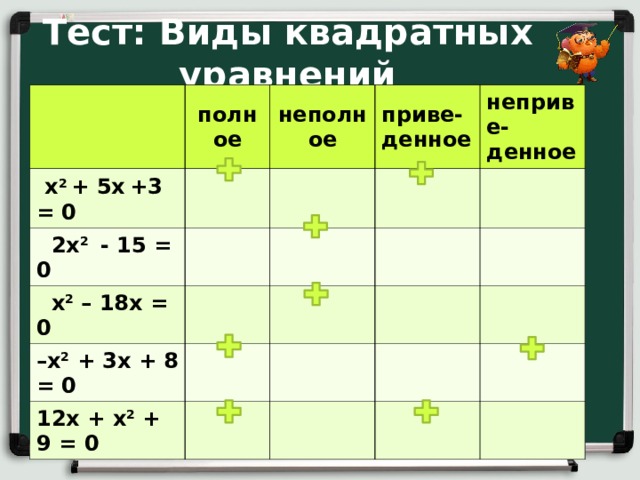
Тест: Виды квадратных уравнений
х 2 + 5х +3 = 0
полное
неполное
2х 2 — 15 = 0
приве-
денное
х 2 – 18х = 0
неприве-
денное
– х 2 + 3х + 8 = 0
12х + х 2 + 9 = 0
Вычеркните лишнее уравнение
x² – 10 x = 0,
3 x² – х + 7 = 0,
9 – x² = 0,
16 x² = 0.
x² – 4 x + 2 = 0,
x² + 6 x – 5 = 0,
8 x² – 9 x – 3 = 0
x² + 4 x + 3 = 0.
3 x² – 2x – 1 = 0
x² + 7 x – 3 = 0,
4 x² + 9x – 1 3 =0
x² – 5 x = 0.
Основные методы решения квадратных уравнений
- С помощью формул корней квадратного уравнения
- С помощью формул корней для чётного коэффициента b
- С помощью теоремы Виета: Если х 1 и х 2 корни приведённого квадратного уравнения х² + px + q = 0 , то x 1 + x 2 = — p , а x 1 x 2 = q .
Франсуа Виет 1540-1603
французский математик, основоположник символической алгебры. По образованию и основной профессии — юрист.
Найдите коэффициенты в и с квадратного уравнения
x ² x = 0
если а) x 1 + x 2 = — 4 , x 1 x 2 = 9 ;
б) x 1 + x 2 = 7 , x 1 x 2 = 3 .
Приёмы устного решения квадратных уравнений
ПО СВОЙСТВУ КОЭФФИЦИЕНТОВ:
a x 2 + b x + c = 0
1. Если a + b + c = 0 , то один
корень уравнения x 1 = 1 , а второй
x 2 = c / a .
Пример : 2 x ² — 3 x + 1 = 0;
2 – 3 + 1 = 0, поэтому x 1 = 1, x 2 = 1/2
Приёмы устного решения квадратных уравнений
ПО СВОЙСТВУ КОЭФФИЦИЕНТОВ:
a x 2 + b x + c = 0
- Если a + c = b , то один корень уравнения x 1 = — 1 , а второй
x 2 = — c / a .
Пример : 2 x ² + 3 x + 1 = 0;
2 + 1 = 3, поэтому x 1 = — 1, x 2 = — 1/2
Приёмы устного решения квадратных уравнений
213х 2 + 2013х + 1800 = 0
Решение:
т.к. 213 + 1800 = 2013, то
x 1 = — 1, x 2 = — 1800/213
Приём «переброски» коэффициентов
2х 2 – 11х + 5 = 0,
«перебрасываем» 2 к 5 как множитель
х 2 – 11х + 10 = 0,
корни полученного уравнения 10 и 1
и теперь их обратно делим на 2,
получаем x 1 = 5, а второй x 2 = 1/2.
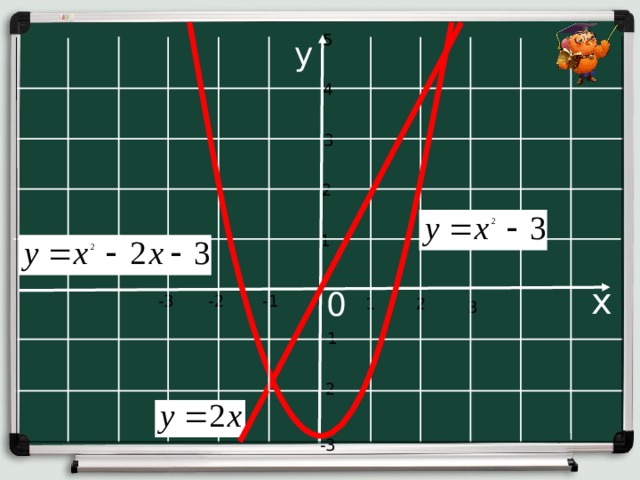
5
у
4
3
2
1
х
0
-2
-3
-1
2
1
3
-1
-2
-3
«Человеку, изучающему алгебру, часто
полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну
задачу различными методами, можно
путем сравнений выяснить, какой из них короче и эффективнее. Так вырабаты-
вается опыт». Уоррен Сойер
